THE CURSE OF DIMENSIONALITY!

Coming soon to a model near you.

The Curse of Dimensionality (see Wikipedia) refers to a certain kind of problems that appear and become severe very fast as we increase the dimension of the space in which the problem is set. An example of critical importance for Machine Learning, related to the density / sparsity of a random sample of size \(n\) as we increase the number of variables in the dataset. Think about the number of empty bins in each of these figures. Note that the nuber of samples is the same (n = 10), while the density (ratio number of samples / number of bins) is, respectively, 2, 0.4, 0.08.

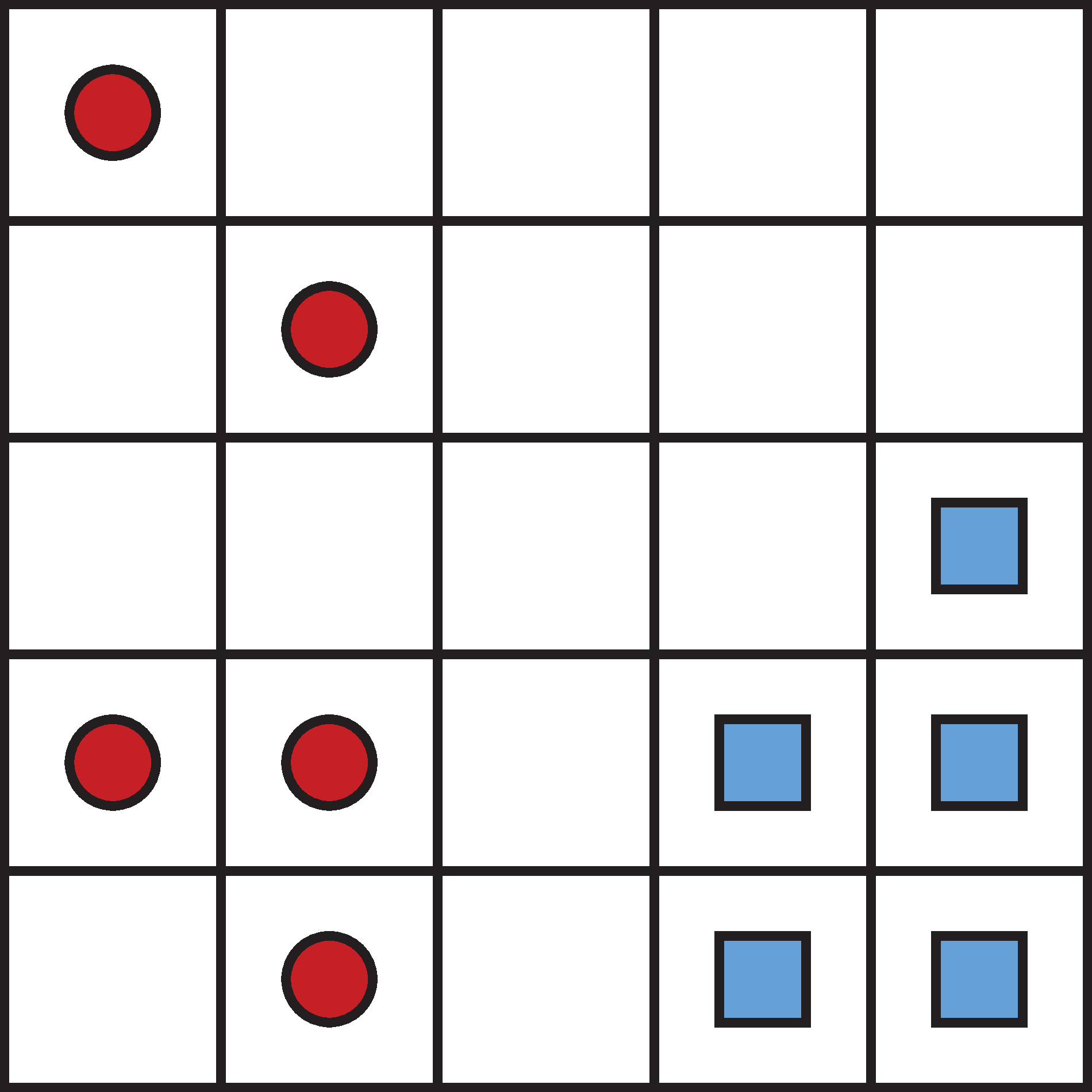
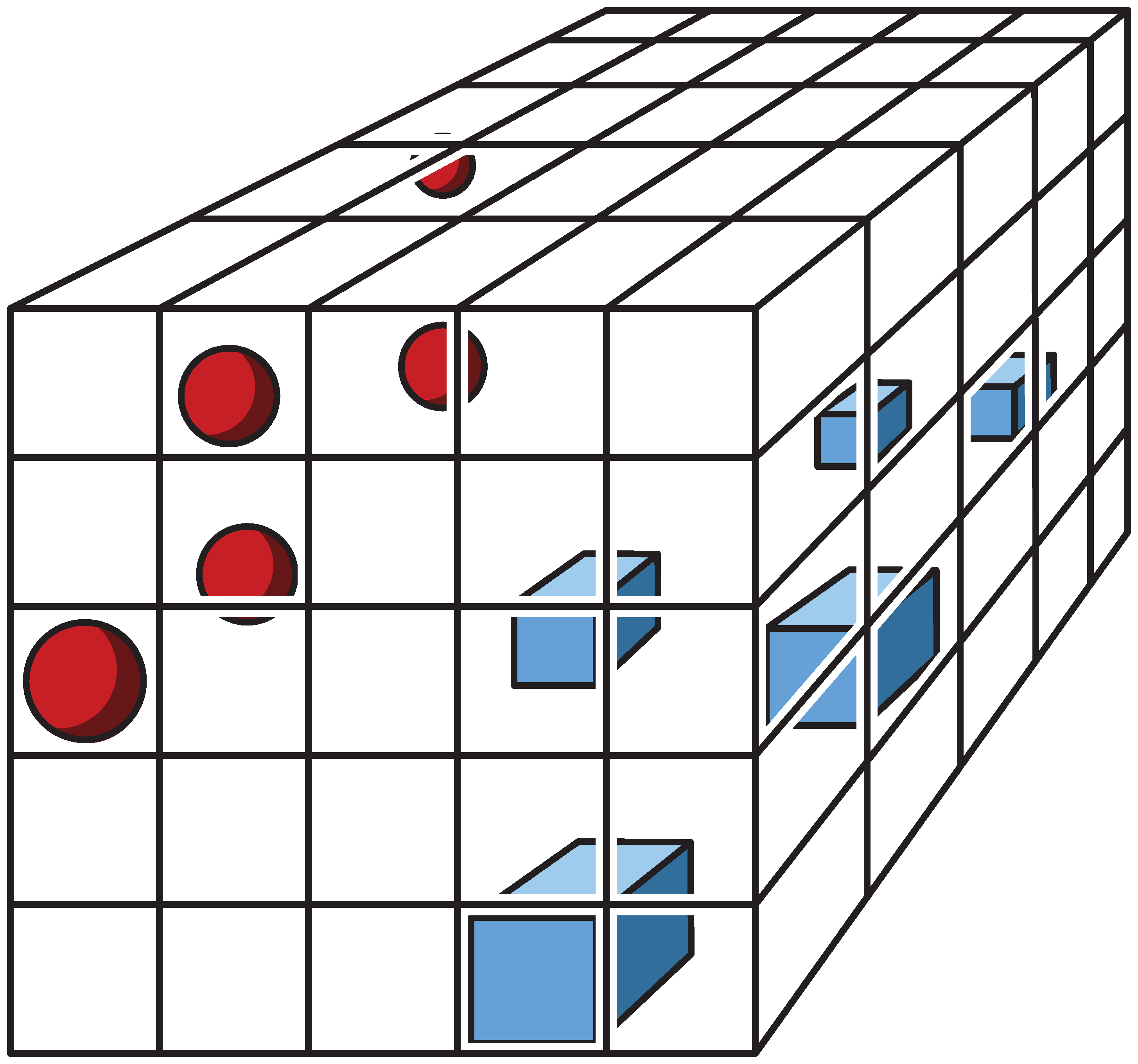
So, by something apparently as innocent as adding two extra variables to our dataset we have actually made the exploration of the sample space much harder.

Source: This example and the illustrating figures are kindly provided (under MIT license) by A. Glassner, and appear in his (highly recommended) book Andrew Glassner (2021) Deep Learning: A Visual Approach. No Starch Press.
The opening image was generated with AI (DALL-E) with the prompt: “can you make the poster for a classic horror movie from the 40s with title The Curse of Dimensionality, starring Random Sample and Machine Learning?”
In Spanish: “¿puedes hacer el cartel de una película de terror clásica de los años 40 titulada The Curse of Dimensionality protagonizada por Random Sample y Machine Learning?”